Brute Forcing Every Manual Round for Prosperity 2

Summary:

Intro
Round 1
- Explanation
- Code
Round 2
- Explanation
- Code
Round 3
- Explanation
- Code
Round 4
- Explanation
- Code

Intro

I signed up for the Prosperity 2 trading challenge and probably spent way more time than I should on it. I was responsible for all manual rounds for our team, and so far (4 rounds in) I have been brute forcing every single round with some batched Python.

Just wanted to share my solutions here, feedback welcomed at davidfeng@uchicago.edu.

Round 1

Trade Objective from Official Site (Click to Expand)

A huge school of goldfish arrived at our shores. And they all brought scuba gear they want to get rid of fast. For the right price of course.

You only have two chances to offer a good price. Each one of the goldfish will accept the lowest bid that is over their reserve price. There's a constant desire for scuba gear on the archipelago. So, at the end of the round, you'll be able to sell them for 1000 SeaShells a piece. Your goal is to set prices that ensure a profitable trade with as many goldfish as possible.

Once you are satisfied with your strategy and input, use the 'Submit manual trade' button to lock it in. Note that you can (re)submit new strategies as long as the round is still in progress. As soon as the round ends, the trading strategy that was submitted last will be processed.

Good luck and have fun trading!

Notes from Wiki (Click to Expand)

With a large school of goldfish visiting, an opportunity arises to acquire some top grade scuba gear. You only have two chances to offer a good price. Each one of the goldfish will accept the lowest bid that is over their reserve price. You know there’s a constant desire for scuba gear on the archipelago. So, at the end of the round, you’ll be able to sell them for 1000 SeaShells a piece.

Whilst not every goldfish has the same reserve price, you know the distribution of their reserve prices. The reserve price will be no lower than 900 and no higher than 1000. The probability scales linearly from 0 at 900 to most likely at 1000.

You only trade with the goldfish. Bids of other participants will not affect your results.

Think hard about how you want to set your two bids in order to walk away with some serious SeaShell profit.

Round 1 Explanation

This is not a terribly difficult question. The hardest part is probably to articulate how profit is calculated. Here is a brief summary:

We set two bids / prices, 1 low 1 high
We buy from all goldfish who are willing to sale for the lower bid
- If the low bid is a, then we buy from all goldfish with reserve price p <= a
- We pay our price a and not the goldfish's reserve price p, making profit 1000-a on each sell
We buy from all goldfish who are willing to sale for the higher bid
- If the high bid is b, then we buy from all goldfish with reserve price a < p <= b (Goldfish with p <= a have already sold)
- We pay our price b and not the goldfish's reserve price p, making profit 1000-b on each sell

In short, there we first buy everything below our lowest bid, and afterwards be buy everything below our highest bid.

With this understanding, it is simple enough to just Monte Carlo the results. Note that we can draw samples from a given distribution with numpy.random.triangular function, where we set the left (lower limit) to 900, and both mode and right (higher limit) to 1000. Here is an excerpt from the official Numpy documentation:

random.triangular(left, mode, right, size=None)
Draw samples from the triangular distribution over the interval [left, right].
The triangular distribution is a continuous probability distribution with lower limit left, peak at mode, and upper limit right. Unlike the other distributions, these parameters directly define the shape of the pdf.

With the information above, we ran 200 simulations with 10,000 gold fishes each, keeping track of the best pair of bids. Here is the output:

Lower Bid Statistics
Min: 945,
Max: 957,
Median: 952.0,
Average: 951.61,
Std Deviation: 2.5880301389280613
----------
Higher Bid Statistics
Min: 972,
Max: 983,
Median: 978.0,
Average: 978.125,
Std Deviation: 1.8545552027373033

Round 1 Code

The full expanded code takes up too much space, so I made each code cell expandable. If you don't want to copy-paste each cell, here is a ready-to-run Colab Notebook with everything in it.

Define Constants

N_SIMULATIONS = 200  # Number of simulations to run

PRICE = 1000 # Selling price per scuba gear
MIN_RESERVE_PRICE = 900 # Minimum reserve price of the goldfish
MAX_RESERVE_PRICE = 1000 # Maximum reserve price of the goldfish
N_GOLDFISHES = 10000 # Number of individuals to model in each simulation for precision

Import Libraries

import numpy as np
import matplotlib.pyplot as plt

Helper Functions

# Function to simulate bids and calculate profits
def simulate_bids(verbose = True):
    best_pair = (0, 0)  # To store the best bid combination
    best_profit = 0  # To store the maximum profit found

    # Iterate through all possible combinations of bids within the valid range
    for low_bid in range(MIN_RESERVE_PRICE, MAX_RESERVE_PRICE):
        for high_bid in range(low_bid + 1, MAX_RESERVE_PRICE + 1):

            profit = 0  # Reset profit for each bid combination

            # Simulate each goldfish's reserve price
            for reserve_price in np.random.triangular(MIN_RESERVE_PRICE, MAX_RESERVE_PRICE, MAX_RESERVE_PRICE, N_GOLDFISHES):

                # Check if the goldfish will accept the low bid
                if reserve_price <= low_bid:
                    profit += (PRICE - low_bid)

                # Check if the goldfish will accept the high bid
                elif reserve_price <= high_bid:
                    profit += (PRICE - high_bid)

            # Update best bid combination if the current one is more profitable
            if profit > best_profit:
                best_profit = profit
                best_pair = (low_bid, high_bid)
                if verbose:
                  print(f"\rProfit:{profit}\tLow:{low_bid}\tHigh:{high_bid}", end = "")

    return best_pair, best_profit

# Function to print statistics given an array like input

def summary_stats(arr, name = ""):
print("\n" + "-"\*10)

    if name:
      print(name)

    print((
        f"Min: {np.min(arr)},\n"
        f"Max: {np.max(arr)},\n"
        f"Median: {np.median(arr)},\n"
        f"Average: {np.mean(arr)},\n"
        f"Std Deviation: {np.std(arr)}"
    ), end = "")

Justify "np.random.triangular" gives desired distribution (Optional)

h = plt.hist(
    np.random.triangular(MIN_RESERVE_PRICE, MAX_RESERVE_PRICE, MAX_RESERVE_PRICE, N_GOLDFISHES),
    bins=200,
    density=True
)

plt.show()

Run Simulation

#@title Run Simulation

small_bids = []
large_bids = []
profits = []

for i in range(N_SIMULATIONS):
print(f"\n{i+1}/{N_SIMULATIONS}")
pair, profit = simulate_bids()
small_bids.append(pair[0])
large_bids.append(pair[1])
profits.append(profit)

summary_stats(small_bids, "Lower Bid Statistics")
summary_stats(large_bids, "Higher Bid Statistics")
summary_stats(profits, "Max Profit Statistics")

Round 2

Trade Objective from Official Site (Click to Expand)

Today is a special day. Representatives from three other archipelagos are visiting to trade their currencies with us. You can trade Wasabi roots with Sing the Songbird, Pizza slices with Devin the Duck, and Snowballs with Pam the Penguin.

Your objective is to trade these currencies and maximize your profit in SeaShells. The number of trades is limited to 5. You must begin your first trade and end your last trade with our own currency; SeaShells. Use the trading table to develop your trading strategy, and use the drop down fields to translate your strategy into actionable input. Once you are satisfied with your strategy and input, use the 'Submit manual trade' button to lock it in.

Note that you can (re)submit new strategies as long as the round is still in progress. As soon as the round ends, the trading strategy that was submitted last will be processed.

Good luck and have fun trading!

Notes from Wiki (Click to Expand)

You get the chance to do a series of trades in some foreign island currencies. The first trade is a conversion of your SeaShells into a foreign currency, the last trade is a conversion from a foreign currency into SeaShells. Everything in between is up to you. Give some thought to what series of trades you would like to do, as there might be an opportunity to walk away with more shells than you arrived with.

Round 2 Explanation

This is the easiest round so far. We just need to brute force over all currencies / products and fill in the blank:

Seashell -> [?] -> [?] -> [?] -> [?] -> Seashell

Do note that we don't have to do all 5 trades, so we also maximize over:

Seashell -> [?] -> [?] -> [?] -> Seashell

Seashell -> [?] -> [?] -> Seashell

Seashell -> [?] -> Seashell

Each unknown blank have 4 possibilities, that leaves us with a total of

$4^4+4^3+4^2+4^1 = 340$

total possibilities, out of which we will pick the one to maximize the final amount of seashells.

Here is the final output:


Best 4 trades: Shell -> Pizza Slice -> Wasabi Root -> Shell -> Pizza Slice -> Shell
Best profit: 1.0569693888
We start with 2000 Shells.
Then we trade Shell to Pizza Slice at 1 Shell : 1.41 Pizza Slice.
Thus we have 2000 _ 1.41 = 2820.0 Pizza Slices
Then we trade Pizza Slice to Wasabi Root at 1 Pizza Slice : 0.48 Wasabi Root.
Thus we have 2820.0 _ 0.48 = 1353.6 Wasabi Roots
Then we trade Wasabi Root to Shell at 1 Wasabi Root : 1.56 Shell.
Thus we have 1353.6 _ 1.56 = 2111.616 Shells
Then we trade Shell to Pizza Slice at 1 Shell : 1.41 Pizza Slice.
Thus we have 2111.616 _ 1.41 = 2977.3785599999997 Pizza Slices
Then we trade Pizza Slice to Shell at 1 Pizza Slice : 0.71 Shell.
Thus we have 2977.3785599999997 \* 0.71 = 2113.9387776 Shells
Finally, we end up with 2113.9387776 Shells.

Round 2 Code

The full expanded code takes up too much space, so I made each code cell expandable. If you don't want to copy-paste each cell, here is a ready-to-run Colab Notebook with everything in it.

Define Constants

PROD_LST = ['Pizza Slice', 'Wasabi Root', 'Snowball', 'Shell']

CONVERSION_MATRIX = [
    [1.  , 0.48, 1.52, 0.71],
    [2.05, 1.  , 3.26, 1.56],
    [0.64, 0.3 , 1.  , 0.46],
    [1.41, 0.61, 2.08, 1.  ]
]

# Mapping words to index numbers
TO_NUM = {
    "Pizza Slice": 0,
    "Wasabi Root": 1,
    "Snowball": 2,
    "Shell": 3
}

# Mapping index numbers back to words
TO_PROD = {
    0: "Pizza Slice",
    1: "Wasabi Root",
    2: "Snowball",
    3: "Shell"
}

Import Libraries

import numpy as np
from itertools import product

Helper Functions

# Function to simulate moving between currency
def get_profit(list_prod):

    # We can fill in 1-4 currencies
    assert len(list_prod) in [1,2,3,4]

    profit = 1
    list_prod = ["Shell"] + list_prod + ["Shell"]

    # Loop through each pair of currencies
    for i in range(len(list_prod)-1):

        # Convert the current currency to the next one
        cur = TO_NUM[list_prod[i]]
        nxt = TO_NUM[list_prod[i+1]]
        profit *= CONVERSION_MATRIX[cur][nxt]

    return profit, list_prod

# Same as get_profit, but prints out results

def get_profit_verbose(list_prod):

    # Starting with a hardcoded initial amount of 2000 Shells
    initial_amount = 2000
    amount = initial_amount

    # For printing detailed steps
    print(f"We start with {initial_amount} Shells.")

    for i in range(len(list_prod) - 1):
        cur = TO_NUM[list_prod[i]]
        nxt = TO_NUM[list_prod[i+1]]
        rate = CONVERSION_MATRIX[cur][nxt]
        new_amount = amount * rate

        print(f"Then we trade {list_prod[i]} to {list_prod[i+1]} at 1 {list_prod[i]} : {rate} {list_prod[i+1]}.")
        print(f"Thus we have {amount} * {rate} = {new_amount} {list_prod[i+1]}s")

        # Update the amount for the next trade
        amount = new_amount

    # Final output for the amount of Shells we end up with
    print(f"Finally, we end up with {amount} Shells.")
    print("-"*10 + "\n")

    return amount, list_prod

# Function to find maximum profit given a certain number of trades

def run_simulation(trade_count, verbose=False):
print(f"Running {trade_count} currencies / {trade_count+1} trades...", end="")
best_profit = 0
best_trades = []

    # Generate all combinations of products with the length of `trade_count`
    for prods in product(PROD_LST, repeat=trade_count):
        profit, list_prod = get_profit(list(prods))
        if profit > best_profit:
            best_profit = profit
            best_trades = list_prod

    print("\rBest {} trades: {}".format(trade_count, " -> ".join(best_trades)))
    print("Best profit:", best_profit)

    if verbose:
        get_profit_verbose(best_trades)

Run Simulation

for trade_count in range(1, 4+1):
    run_simulation(trade_count, verbose=True)

Round 3

Trade Objective from Official Site (Click to Expand)

A mysterious message in a bottle washed ashore. It turns out to contain a treasure map belonging to the legendary Iguana Jones. Apparently, bounty is scattered all over the archipelago. The adventurer-archeologist also left a note with the treasure map containing some hints on how to find the biggest treasures and how to keep them to yourself.

Your goal is to choose up to three expedition destinations and take home the most treasure. Each tile is said to hold at least 7.5k SeaShells, but rumors are going around that there might be multiple chests in one tile. Select your preferred destination(s) by clicking on the treasure map. There might be costs involved in undertaking these expeditions and you are not the only one looking for treasure. So choose your expeditions and destinations thoughtfully.

Good luck and have fun exploring!

Notes from Wiki (Click to Expand)

A mysterious treasure map and accompanying note has everyone acting like heroic adventurers. You get to go on a maximum of three expeditions to search for treasure. Your first expedition is free, but the second and third one will come at a cost. Keep in mind that you are not the only one searching and you’ll have to split the spoils with all the others that search in the same spot. Plan your expeditions carefully and you might return with the biggest loot of all.

Here's a breakdown of how your profit from an expedition will be computed: Every spot has its treasure multiplier (up to 100) and the number of hunters (up to 8). The spot's total treasure is the product of the base treasure (7500, same for all spots) and the spot's specific treasure multiplier. However, the resulting amount is then divided by the sum of the hunters and the percentage of all the expeditions (from other players) that took place there. For example, if a field has 5 hunters, and 10% of all the expeditions (from all the other players) are also going there, the prize you get from that field will be divided by 15. After the division, expedition costs apply (if there are any), and profit is what remains.

Second and third expeditions are optional: you are not required to do all 3. Fee for embarking upon a second expedition is 25,000, and for third it's 75,000. Order of submitted expeditions does not matter for grading.

Round 3 Explanation

This round is when things really start to get interesting. There is not a single correct answer, since then everyone will choose it, making the correct answer worse and other strategies better. Instead, we want to find a equilibrium distribution where everybody is making the same profit.

In order to do that, we begin with a long vector with one entry for each possible choice. That is, one entry may represent the percentile of players who chose [(0,1)] and another may represent the percentile of players who chose [(0,1), (3,2), (1,1)]. Note that the order is not important here.

We are essientially looking for such a vector $\vec{V}$ with the following characteristics:

All entries of $\vec{V}$ are non-negative numbers in range $[0, 100]$ such that: $\sum v_i = 100$
Given two arbitrary entries $v_i$ and $v_j$ , one of the following cases hold:
a. The marginal profit of $v_i$ and $v_j$ are the same.
b. The marginal profit of $v_i$ is smaller than that of $v_j$ , and $v_i = 0$ (Or the other way around).

The marginal profit of $v_i$ corresponding to choices $C_i = \{c_{i1}, c_{i2}, ...\}$ can be calculated with the following functions:

\text{Total Profit}(v_i) = \begin{cases} \text{Profit}(c_{i1}) & |C_i| = 1\\ \text{Profit}(c_{i1}) + \text{Profit}(c_{i2}) - 25000 & |C_i| = 2\\ \text{Profit}(c_{i1}) + \text{Profit}(c_{i2}) + \text{Profit}(c_{i3}) - 100000 & |C_i| = 3\\ \end{cases}

\text{Profit}(c_{ij}) = \dfrac{7500 \times \text{Multiplier}_{ij}}{\text{Hunters}_{ij} + \bar{V}_{ij}} \quad \text{Where $\bar{V}_{ij}$ is the sum of all normalized percentiles $v_k$ with $c_{ij}\in C_k$}

Note that since many choices include multiple islands, we need to process it accordingly and not double count anything. As a result, we define $\bar{V}_{ij}$ as such:

\bar{V}_{ij} = \frac{100}{\sum |C_i|v_i} \times \sum_{c_{ij}\in C_k} v_k

The above equation may seems confusing, but the idea is simple:

$\sum |C_i|v_i$ accounts for the number of islands (e.g. If $v_i$ has 3 islands then $|C_i|=3$ ). By normalizing with this term, we make sure we are getting the percentage of island choices instead of the percentage of submitted strategies / players who chose a choice that consists of the given island, which is quite different than what we are looking for.

After we formulated the problem, we can brute force it. To be more specific, we repeat the following steps:

Iterate through all pairs $(v_i, v_j)$ such that $v_i \neq v_j$
Compare if they satisfy one of the following cases:
a. $v_i$ and $v_j$ makes same money
b. $v_i$ makes less but $v_i = 0$ , or vice versa with $v_j$
If not, update $(v_i, v_j)$ with a given step size $\delta$ that counters the unbalance
a. For instance, if $v_i$ makes less money, we subtract $\delta$ from $v_i$ and add it to $v_j$ , so $v_i$ makes more money
b. We technically add $min(\delta, v_i)$ to prevent negative probability
Repeat the steps for as many steps as possible, update $\delta$ to be smaller if necessary

As the simulation goes on, we plotted the state of each iteration and got a pretty cool GIF for the effect of step size $\delta$ . We start the delta at $1.0$ and divide it by ten every 50 iterations.

In the order of top-left, top-right, bottom-left, bottom-right, we have 4 different plots:

Top-left plots profit for choices with a None Zero probability in the current distribution.

Top-right plots profit for choices with a Zero probability in the current distribution.

Bottom-left combines the two top plots, plotting top-left in yellow and top-right in blue.

Bottom-right gives the current probability distribution. X-axis is the indexes for unique choices, and Y-axis is the percent of players who chose it. All choices on the X axis are sorted in order. Indices $[0-24]$ are 1 island choices, $[25-324]$ are 2 island choices, and $[325-2624]$ are 3 island choices.

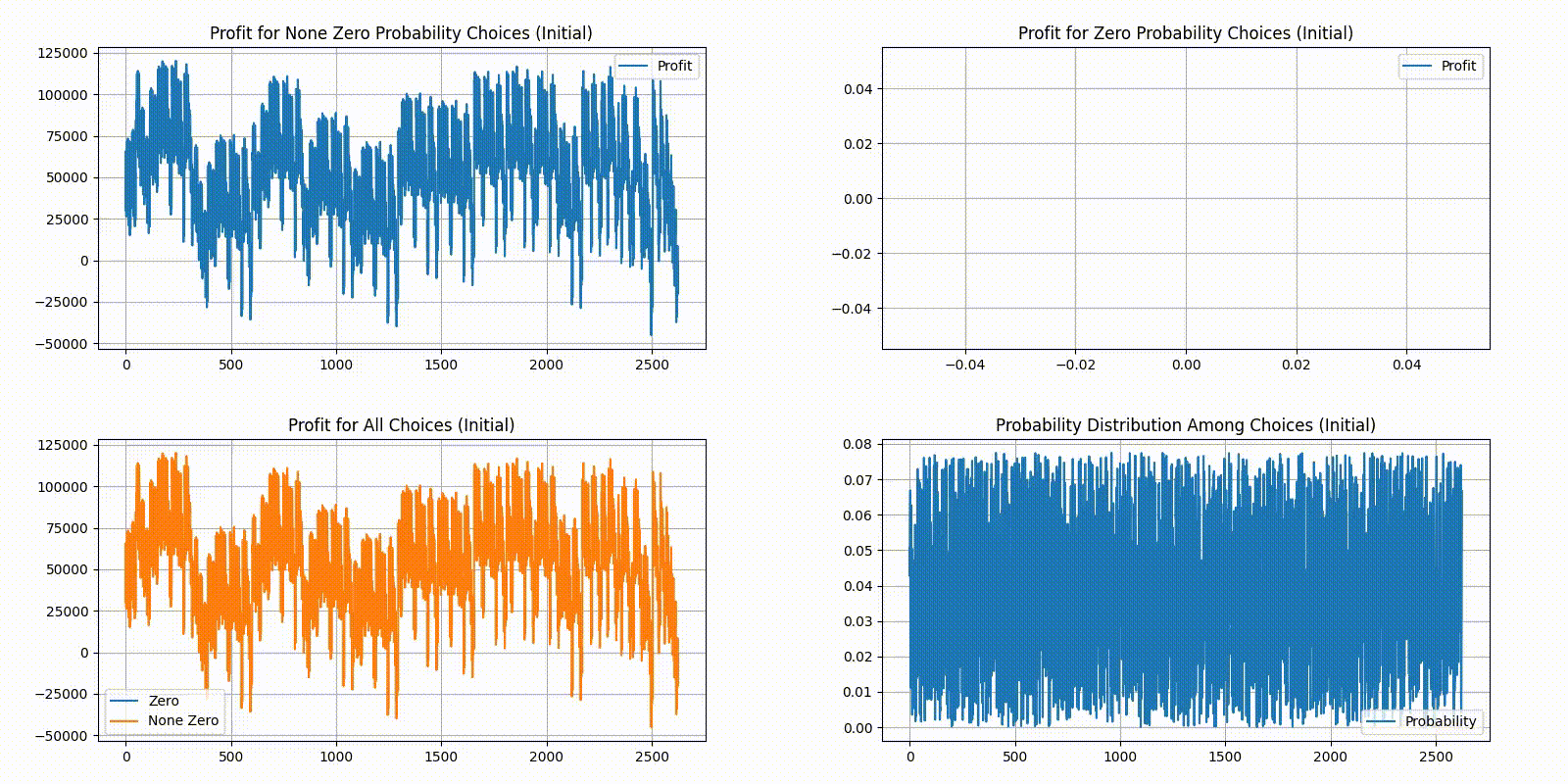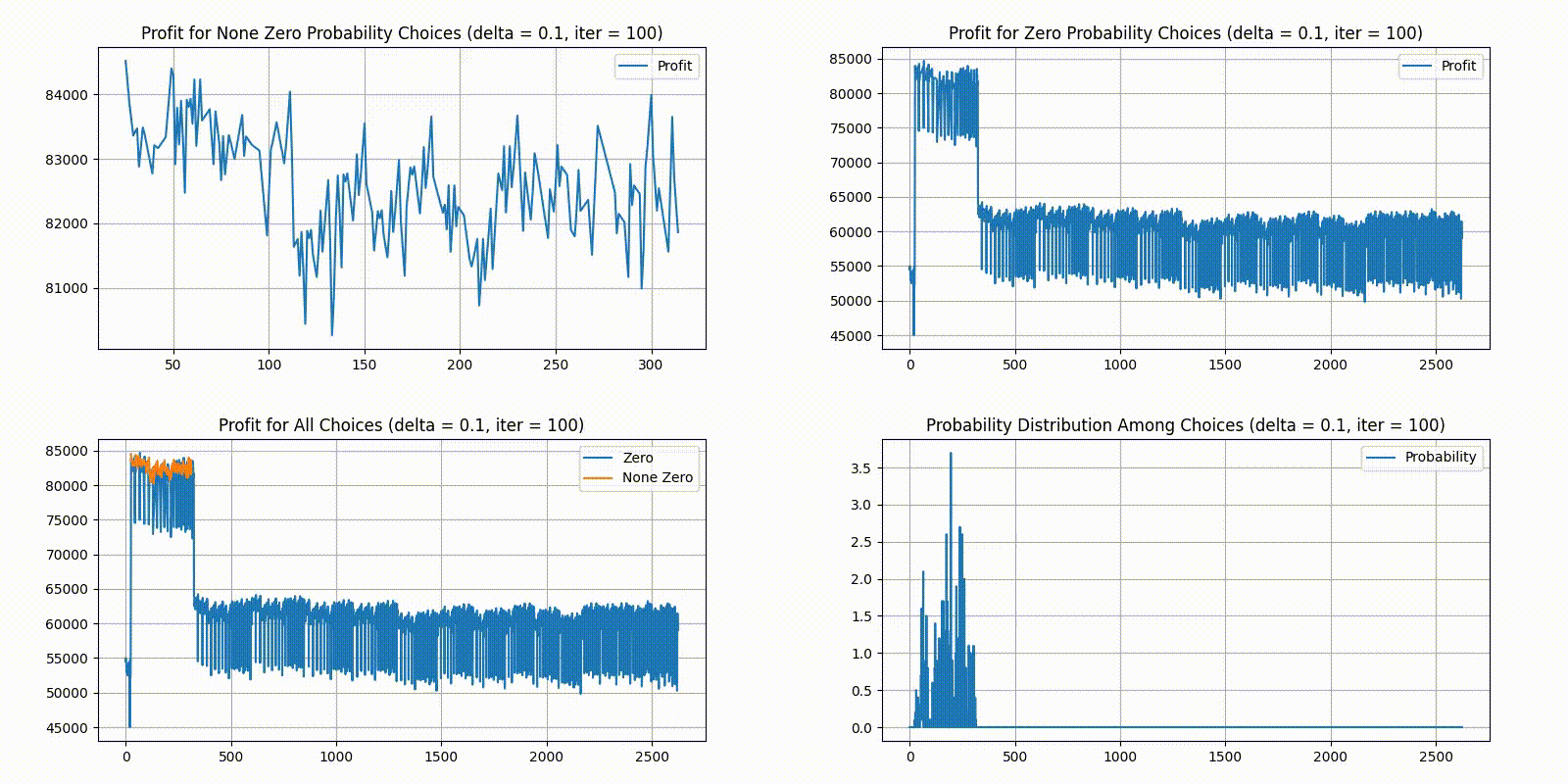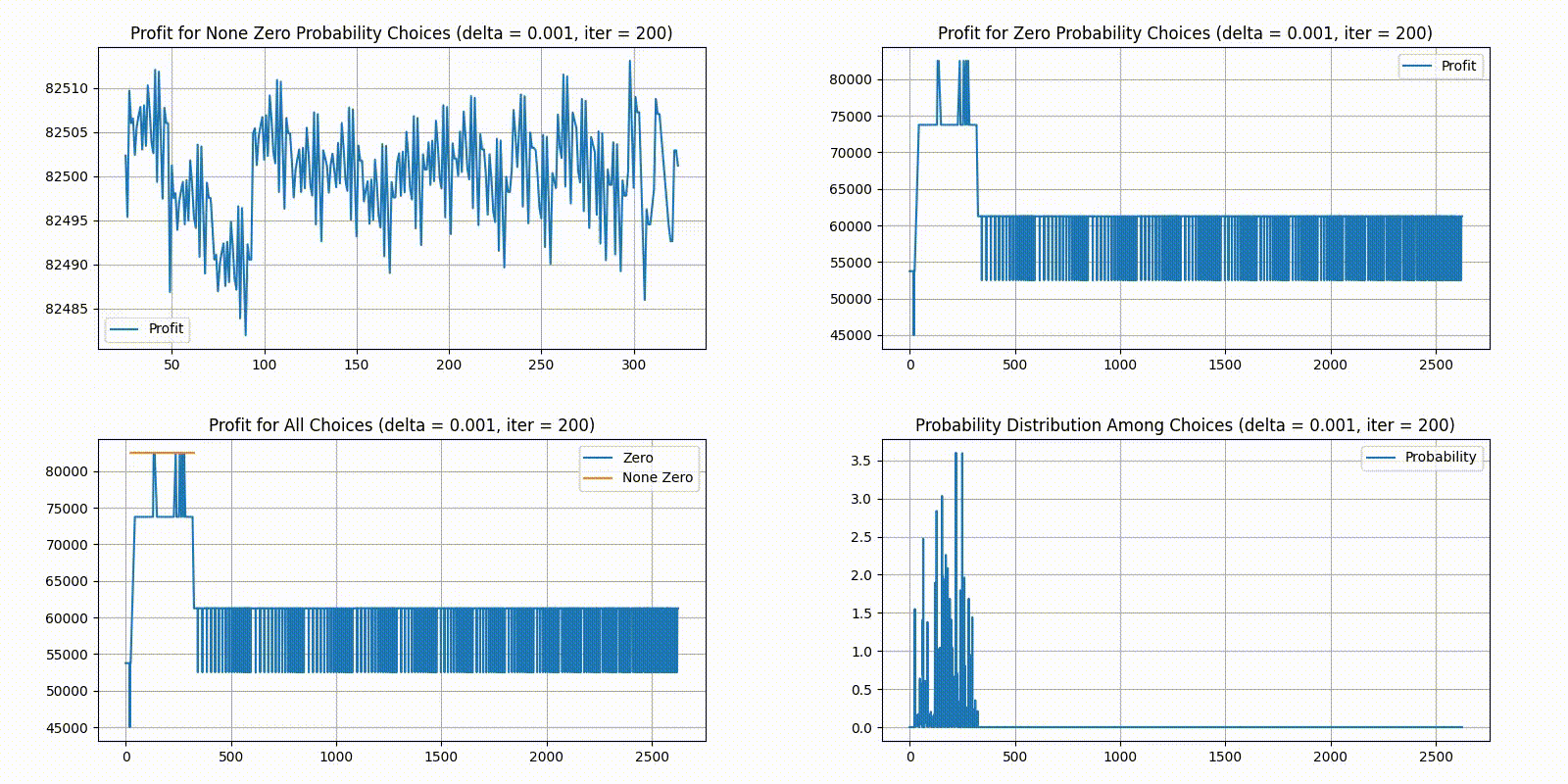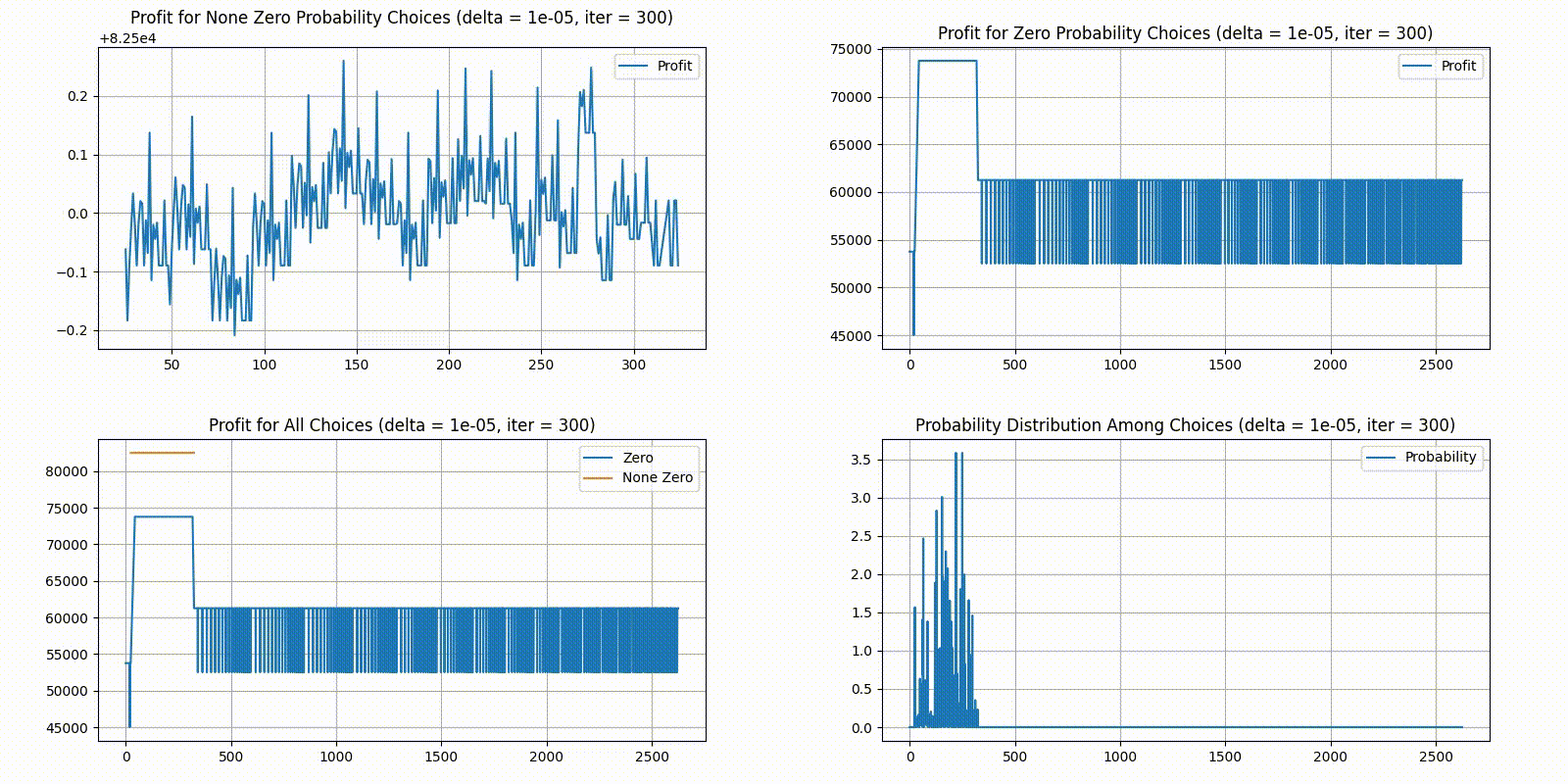
As we can see, choosing 2 islands is generally the optimal solution. As the step size $\delta$ decreases, the distribution quickly stabilizes. Here are the statistics for the final distribution:

Top 10 choices:
[(2, 0), (2, 1)] 3.5850499999999106
[(2, 2), (3, 1)] 3.583449999999967
[(1, 1), (1, 2)] 3.0079899999998894
[(0, 4), (3, 3)] 2.830099999999941
[(0, 1), (3, 3)] 2.4663899999999828
[(1, 2), (1, 3)] 2.2960000000000513
[(1, 2), (3, 2)] 2.073439999999967
[(2, 3), (3, 0)] 1.996660000000012
[(1, 1), (2, 1)] 1.9702600000000208
[(1, 1), (3, 2)] 1.9034099999999843
----------------------------------------
Bottom 10 choices that still have nonezero probability:
[(0, 4), (2, 4)] 0.00012000000000000002
[(3, 1), (4, 3)] 0.00016
[(4, 1), (4, 3)] 0.00026000000000000003
[(2, 4), (3, 3)] 0.0002900000000000001
[(1, 0), (3, 3)] 0.00030000000000000014
[(3, 4), (4, 3)] 0.00031000000000000016
[(3, 0), (4, 3)] 0.0004000000000000004
[(1, 3), (4, 4)] 0.0004300000000000005
[(2, 1), (2, 4)] 0.0006500000000000011
[(0, 2), (4, 3)] 0.0007100000000000008

We ended up intentionally choosing a relatively bad choice though, staying out of the top and bottom 20%.

The idea is less people will choose it so we can reap all benefits ourselves.

Given Answer: [(1, 0), (3, 4)]
The answer is in the 92.55th percentile among all entries.
The answer is in the 29.17th percentile among non-zero entries.

Round 3 Code

The full expanded code takes up too much space, so I made each code cell expandable. If you don't want to copy-paste each cell, here is a ready-to-run Colab Notebook with everything in it.

Import Libraries & Set Up Output Folder

import os
import cv2
import time
import json
import random
import imageio
import itertools

import numpy as np
import matplotlib.pyplot as plt

OUTPUT_NAME = "prosperity_240415_round3_manual_optimal_distribution_output"

try:
os.makedirs(OUTPUT_NAME)
except OSError:
if not os.path.isdir(OUTPUT_NAME):
raise

Define Constants

SHELL_PER_MULTIPLIER = 7500
EXPEDITION_COSTS = {1: 0, 2: 25000, 3: 100000}

# (i,j) stands for i multiplier and j hunters
TREASURE_MAP = [
    [(24, 2), (70, 4), (41, 3), (21, 2), (60, 4)],
    [(47, 3), (82, 5), (87, 5), (80, 5), (35, 3)],
    [(73, 4), (89, 5), (100, 8), (90, 7), (17, 2)],
    [(77, 5), (83, 5), (85, 5), (79, 5), (55, 4)],
    [(12, 2), (27, 3), (52, 4), (15, 2), (30, 3)]
]

# All possible single islands (NOT ALL CHOICES)
ISLANDS = [(i, j) for i in range(5) for j in range(5)]

# All possible choices, also weights |C_i| for islands
CHOICES = []
WEIGHTS = []
for l in itertools.combinations(ISLANDS, 1):
    CHOICES.append(list(l))
    WEIGHTS.append(1.0)
for l in itertools.combinations(ISLANDS, 2):
    CHOICES.append(list(l))
    WEIGHTS.append(2.0)
for l in itertools.combinations(ISLANDS, 3):
    CHOICES.append(list(l))
    WEIGHTS.append(3.0)

# np.array allows faster processing
# Not available for CHOICES, which does not have uniform length :(
WEIGHTS = np.array(WEIGHTS)

# Masks for calculating sum of v_k, True iff island is in the choice
# Caching it with dict accelerates function by ~1e3 times
MASKS = {}
for island in ISLANDS:
    MASKS[island] = np.array([island in choice for choice in CHOICES])

Helper Functions

# Get the profit for a single island
def profit_island(island, mask, v, weight):
    # sum_v is V bar or normalized sum
    sum_v = np.sum(v[mask]) / weight * 100
    i, j = island
    multiplier, hunters = TREASURE_MAP[i][j]
    return SHELL_PER_MULTIPLIER * multiplier / (hunters + sum_v)

# Get the profit for a choice

def total_profit(choice, v, weight):
profit = 0
for island in choice:
mask = MASKS[island]
profit += profit_island(island, mask, v, weight)
return profit - EXPEDITION_COSTS[len(choice)]

# Remaining are just plotting functions

def plot_none_zero_probability(v, name='Profit from choices with none zero probability'):
weight = np.dot(v, WEIGHTS)
x = [i for i in range(len(v)) if v[i]>0]
y = [total_profit(CHOICES[i], v, weight) for i in range(len(v)) if v[i]>0]

    plt.figure(figsize=(8, 4))
    plt.plot(x, y, label='Profit')
    plt.title(name)
    plt.grid(True)
    plt.legend()
    plt.savefig(f'{name}.png')

def plot_zero_probability(v, name='Profit from choices with zero probability'):
weight = np.dot(v, WEIGHTS)
x = [i for i in range(len(v)) if v[i]==0]
y = [total_profit(CHOICES[i], v, weight) for i in range(len(v)) if v[i]==0]

    plt.figure(figsize=(8, 4))
    plt.plot(x, y, label='Profit')
    plt.title(name)
    plt.grid(True)
    plt.legend()
    plt.savefig(f'{name}.png')

def plot_both_profit(v, name='Profit from both, in the same chart'):
weight = np.dot(v, WEIGHTS)

    x1 = [i for i in range(len(v)) if v[i]==0]
    y1 = [total_profit(CHOICES[i], v, weight) for i in range(len(v)) if v[i]==0]

    x2 = [i for i in range(len(v)) if v[i]>0]
    y2 = [total_profit(CHOICES[i], v, weight) for i in range(len(v)) if v[i]>0]

    plt.figure(figsize=(8, 4))
    plt.plot(x1, y1, label='Zero')
    plt.plot(x2, y2, label='None Zero')
    plt.title(name)
    plt.grid(True)
    plt.legend()
    plt.savefig(f'{name}.png')

def plot_probability(v, name='Probability Distribution among all possible choices'):
x = [i for i in range(len(v))]
y = [i for i in v]

    plt.figure(figsize=(8, 4))
    plt.plot(x, y, label='Probability')
    plt.title(name)
    plt.grid(True)
    plt.legend()
    plt.savefig(f'{name}.png')

def plot(v, n1, n2, n3, n4):
plot_none_zero_probability(v, n1)
plot_zero_probability(v, n2)
plot_both_profit(v, n3)
plot_probability(v, n4)

    image = cv2.vconcat([
        cv2.hconcat([cv2.imread(f'{n1}.png'), cv2.imread(f'{n2}.png')]),
        cv2.hconcat([cv2.imread(f'{n3}.png'), cv2.imread(f'{n4}.png')]),
    ])

    cv2.imwrite("result.png", image)
    plt.close("all")
    return imageio.v2.imread("result.png")

Run Simulation

# Initialize distribution vector with small random values summing to 100%
random_values = np.random.rand(len(CHOICES))
v = 100 * random_values / np.sum(random_values)

# The settings describe the delta iteration pairs
# (0.1, 20) means perform 20 iterations with delta=0.1
# After each delta iteration pair a checkpoint is saved
# Note that a iteration is described as iterating through all the pairs once
settings = np.array([
    (1.0, 50),
    (0.1, 50),
    (0.01, 50),
    (0.001, 50),
    (0.0001, 50),
    (0.00001, 50),
])

# Time for logging and frames for plotting
init_time = time.time()
frame_lst = []

# Plotting
frame_lst.append(
    plot(
        v,
        "Profit for None Zero Probability Choices (Initial)",
        "Profit for Zero Probability Choices (Initial)",
        "Profit for All Choices (Initial)",
        "Probability Distribution Among Choices (Initial)"
    )
)

# Iterate through settings
counter = 0
checkpoint_counter = 0
for delta_value, num_iterations in settings:
    num_iterations = int(num_iterations)
    checkpoint_counter += num_iterations
    for iter in range(num_iterations):

        counter += 1

        # Time for logging
        round_time = time.time()

        # Iterate through pairs
        for i in range(len(v)):
            for j in range(len(v)):

                # Choose two different indices
                if i == j:
                    continue

                # Matrices soon become sparse, utilize it for speed boost
                if v[i]==0 and v[j]==0:
                    continue

                # V bar in equation above
                # Calculate once and apply to both profit calculations
                weight = np.dot(v, WEIGHTS)

                # Find profit, update probability accordingly
                profit_i = total_profit(CHOICES[i], v, weight)
                profit_j = total_profit(CHOICES[j], v, weight)

                if profit_i < profit_j and v[i] > 0:
                    delta = min(v[i], delta_value)
                    v[i] -= delta
                    v[j] += delta
                elif profit_i > profit_j and v[j] > 0:
                    delta = min(v[j], delta_value)
                    v[j] -= delta
                    v[i] += delta

        # Logging
        print(f"-"*40)
        print(f"Step Size = {delta_value} | Iteration {counter}/{checkpoint_counter}")
        print(f"Iteration Time:", time.strftime('%H hr %M min %S s', time.gmtime(time.time() - round_time)))
        print(f"Total Time:", time.strftime('%H hr %M min %S s', time.gmtime(time.time() - init_time)))

        # Plotting
        frame_lst.append(
            plot(
                v,
                f"Profit for None Zero Probability Choices (delta = {delta_value}, iter = {counter})",
                f"Profit for Zero Probability Choices (delta = {delta_value}, iter = {counter})",
                f"Profit for All Choices (delta = {delta_value}, iter = {counter})",
                f"Probability Distribution Among Choices (delta = {delta_value}, iter = {counter})"
            )
        )

    # Save Checkpoint
    with open(f'{OUTPUT_NAME}/checkpoint_{counter}.txt', 'w') as filehandle:
        json.dump(list(v), filehandle)

        imageio.mimsave(f'{OUTPUT_NAME}/checkpoint_{counter}.gif', frame_lst, fps=4, loop=2)

    print(f"-"*40)
    print(f"Updated checkpoint at iteration {counter}, saved to folder {OUTPUT_NAME}")

Check If Result is Roughly an Equilibrium (Optional)

def check(v):
    weight = np.dot(v, WEIGHTS)
    for i in range(len(v)):
        for j in range(len(v)):

            # Choose two different indices
            if i == j:
                continue

            # Make sure one is zero and one is not
            if v[i]==0 and v[j]==0:
                continue
            if v[i]!=0 and v[j]!=0:
                continue

            # Swap so i is zero / bad choice
            if v[i]!=0:
                i,j = j,i

            # Compare profits
            profit_i = total_profit(CHOICES[i], v, weight)
            profit_j = total_profit(CHOICES[j], v, weight)

            # This should NOT print anything if we have a stable equilibrium
            if profit_i > profit_j:
                print("NOT EQUILIBRIUM!")
                print(f"Index {i} or choice {CHOICES[i]} has profit {profit_i} and probability {v[i]}")
                print(f"Index {j} or choice {CHOICES[i]} has profit {profit_j} and probability {v[j]}")
                print(f"Although {j} has proability {v[j]} > 0, its profit is lower!")
                return

check(v)

Get Statistics and Sample for Answer

def find_indices_by_count(weights, top_k, bottom_k):
    # Normalize the weights to sum to 1
    probabilities = weights / np.sum(weights)

    # Get indices sorted by probability
    sorted_indices = np.argsort(probabilities)[::-1]  # Descending order
    top_indices = sorted_indices[:top_k]

    # Filter out zero probabilities and get their indices
    non_zero_probabilities = probabilities[probabilities > 0]
    non_zero_sorted_indices = np.argsort(non_zero_probabilities)

    # Select the bottom k indices of non-zero probabilities
    if bottom_k > len(non_zero_sorted_indices):
        bottom_k = len(non_zero_sorted_indices)  # Adjust bottom_k if it's larger than available non-zero indices
    bottom_indices = non_zero_sorted_indices[:bottom_k]

    # Adjust the non-zero indices to match original array indices
    actual_bottom_indices = np.nonzero(probabilities > 0)[0][bottom_indices]

    return top_indices, actual_bottom_indices

def find_percentiles(v, i):
    # Ensure i is within the valid range
    if i >= len(v) or i < 0:
        return None  # or raise an exception

    # Sort the entire array and find the position of v[i]
    sorted_v = np.sort(v)
    position_all = np.argwhere(sorted_v == v[i])[0][0]  # Using argwhere to find the first occurrence
    percentile_all = ((position_all + 0.5) / len(v)) * 100

    # Filter out zero entries and repeat the process
    non_zero_v = v[v != 0]
    sorted_non_zero_v = np.sort(non_zero_v)
    position_non_zero = np.argwhere(sorted_non_zero_v == v[i])[0][0]
    percentile_non_zero = ((position_non_zero + 0.5) / len(non_zero_v)) * 100

    return percentile_all, percentile_non_zero

top_indices, bottom_indices = find_indices_by_count(v, 10, 10)

print(f"-"*40)
print("Top 10 choices:")
for i in top_indices:
    print(CHOICES[i], v[i])

print(f"-"*40)
print("Bottom 10 choices:")
for i in bottom_indices:
    print(CHOICES[i], v[i])

print(f"-"*40)
probabilities = v / np.sum(v)
answer =  np.random.choice(len(v), p=probabilities)
print("Sampled Answer:", CHOICES[answer])
percentile_all, percentile_non_zero = find_percentiles(v, answer)
print(f"The answer is in the {percentile_all:.2f}th percentile among all entries.")
print(f"The answer is in the {percentile_non_zero:.2f}th percentile among non-zero entries.")

Given a Choice, Check the Percentile (Optional)

choice = [(1,0), (3,4)] # Replace with any choice
choice.sort()

# Function to find index of list containing the tuple

def find_index(arr, target_tuple):
for index, list_of_tuples in enumerate(arr):
if any(t == target_tuple for t in list_of_tuples):
return index
return None

def find_percentiles(v, choice):
i = -1
for index, list_of_tuples in enumerate(CHOICES):
if list_of_tuples == choice:
i = index
break

    # Ensure i is within the valid range
    if i >= len(v) or i < 0:
        return None  # or raise an exception

    # Sort the entire array and find the position of v[i]
    sorted_v = np.sort(v)
    position_all = np.argwhere(sorted_v == v[i])[0][0]  # Using argwhere to find the first occurrence
    percentile_all = ((position_all + 0.5) / len(v)) * 100

    # Filter out zero entries and repeat the process
    non_zero_v = v[v != 0]
    sorted_non_zero_v = np.sort(non_zero_v)
    position_non_zero = np.argwhere(sorted_non_zero_v == v[i])[0][0]
    percentile_non_zero = ((position_non_zero + 0.5) / len(non_zero_v)) * 100

    return percentile_all, percentile_non_zero

print("Given Answer:", choice)
percentile_all, percentile_non_zero = find_percentiles(v, choice)
print(f"The answer is in the {percentile_all:.2f}th percentile among all entries.")
print(f"The answer is in the {percentile_non_zero:.2f}th percentile among non-zero entries.")

Convert GIF to MP4 and Save Output (Optional, Colab Only)

!for f in prosperity_240415_round3_manual_optimal_distribution_output/*.gif; do ffmpeg -i "$f" -movflags faststart -pix_fmt yuv420p -vf "scale=trunc(iw/2)*2:trunc(ih/2)*2" -c:v libx264 -preset fast -crf 23 "${f%.*}.mp4"; done

import shutil
shutil.make_archive(OUTPUT_NAME, "zip", OUTPUT_NAME)

from google.colab import files
files.download(f'{OUTPUT_NAME}.zip')

Round 4

Trade Objective from Official Site (Click to Expand)

The goldfish are back. And they brought more scuba gear! Again, they want to get rid of the gear fast and are willing to sell to you for a good price.

You only have two chances to offer a good price. Each one of the goldfish will accept the lowest bid that is over their reserve price. But this time around they heard about what other inhabitants of the archipelago offered last time they visited. So, for your second bid, they also take into account the average of bids by other traders in the archipelago. They'll trade with you when your offer is above the average of all bids. But if you end up under the average, the probability of a deal decreases rapidly.

There's a constant desire for scuba gear on the archipelago. So, at the end of the round, you'll be able to sell them for 1000 SeaShells a piece. Your goal is to set prices that ensure a profitable trade with as many goldfish as possible.

Good luck and have fun trading!

Notes from Wiki (Click to Expand)

The goldfish are back with more scuba gear. Each of the goldfish will have new reserve prices, but they still follow the same distribution as in Round 1.

Your trade options are similar to before. You'll have two chances to offer a good price. Each one of the goldfish will accept the lowest bid that is over their reserve price. But this time, for your second bid, they also take into account the average of the second bids by other traders in the archipelago. They'll trade with you when your offer is above the average of all second bids. But if you end up under the average, the probability of a deal decreases rapidly.

To simulate this probability, the PNL obtained from trading with a fish for which your second bid is under the average of all second bids will be scaled by a factor p:

p = \dfrac{1000 - \text{average bid}}{1000 - \text{your bid}}

What can you learn from the available data and how will you anticipate on this new dynamic? Place your feet firmly in the sand and brace yourself, because this could get messy.

Round 4 Explanation

Our approach to this question is quite similar to Round 3 - we aim to find a good probability vector where everyone makes the same money. However, since we are not using percentiles anymore, the vector can just sum to 1 instead of 100.

We again begin with a long vector with one entry for each possible answer. That is, one entry may represent the percentile of people who chose (900, 1000) and another may represent the percentile of players who chose (925, 975). Note that the order is important here.

We are essientially looking for such a vector $\vec{V}$ with the following characteristics:

All entries of $\vec{V}$ are non-negative numbers in range $[0, 1]$ such that: $\sum v_i = 1$
Given two arbitrary entries $v_i$ and $v_j$ , one of the following cases hold:
a. The profit of $v_i$ and $v_j$ are the same.
b. The profit of $v_i$ is smaller than that of $v_j$ , and $v_i = 0$ (Or the other way around).

The marginal profit of $v_i = (x_i, y_i)$ can be calculatedwith the following functions:

\text{Total Profit}(x_i, y_i) = (1000 - x_i) \cdot G_{[0, x_i]} + p \cdot (1000 - y_i) \cdot G_{[x_i, y_i]}

Where $G_{[a, b]}$ represent the number of goldfishs with reserve price in $[a,b]$ .

We can simply integrate a linear function to get the expected value for $G_{[a, b]}$ , no need for Monte Carlo when we can directly solve the pdf and its integral.

\begin{cases} f(x) = ax+b\\ \int_{900}^{1000}f(x)\ dx = 1\\ f(900) = 0 \end{cases} \implies f(x) = \frac{x}{5000} - \frac{900}{5000} = \frac{x}{5000} - \frac{9}{50}

It is easy to compute integrals of a linear function:

G_{[a,b]} = \int_a^b f(x)\ dx = (b-a)\cdot \dfrac{f(b)+f(a)}{2}

After we formulated the problem, we can brute force it in the same way as before. To be more specific, we repeat the following steps:

Iterate through all pairs $(v_i, v_j)$ such that $v_i \neq v_j$
Compare if they satisfy one of the following cases:
a. $v_i$ and $v_j$ makes same money
b. $v_i$ makes less but $v_i = 0$ , or vice versa with $v_j$
If not, update $(v_i, v_j)$ with a given step size $\delta$ that counters the unbalance
a. For instance, if $v_i$ makes less money, we subtract $\delta$ from $v_i$ and add it to $v_j$ , so $v_i$ makes more money
b. We technically add $min(\delta, v_i)$ to prevent negative probability
Repeat the steps for as many steps as possible, update $\delta$ to be smaller if necessary

We plotted the state of each generation as a GIF, starting the delta at $0.01$ and divide it by ten every 20 iterations. As a reminder, in the order of top-left, top-right, bottom-left, bottom-right, we have 4 different plots:

Top-left plots profit for choices with a None Zero probability in the current distribution.

Top-right plots profit for choices with a Zero probability in the current distribution.

Bottom-left combines the two top plots, plotting top-left in yellow and top-right in blue.

Bottom-right gives the current probability distribution. X-axis is the indexes for unique choices, and Y-axis is the percent of players who chose it.

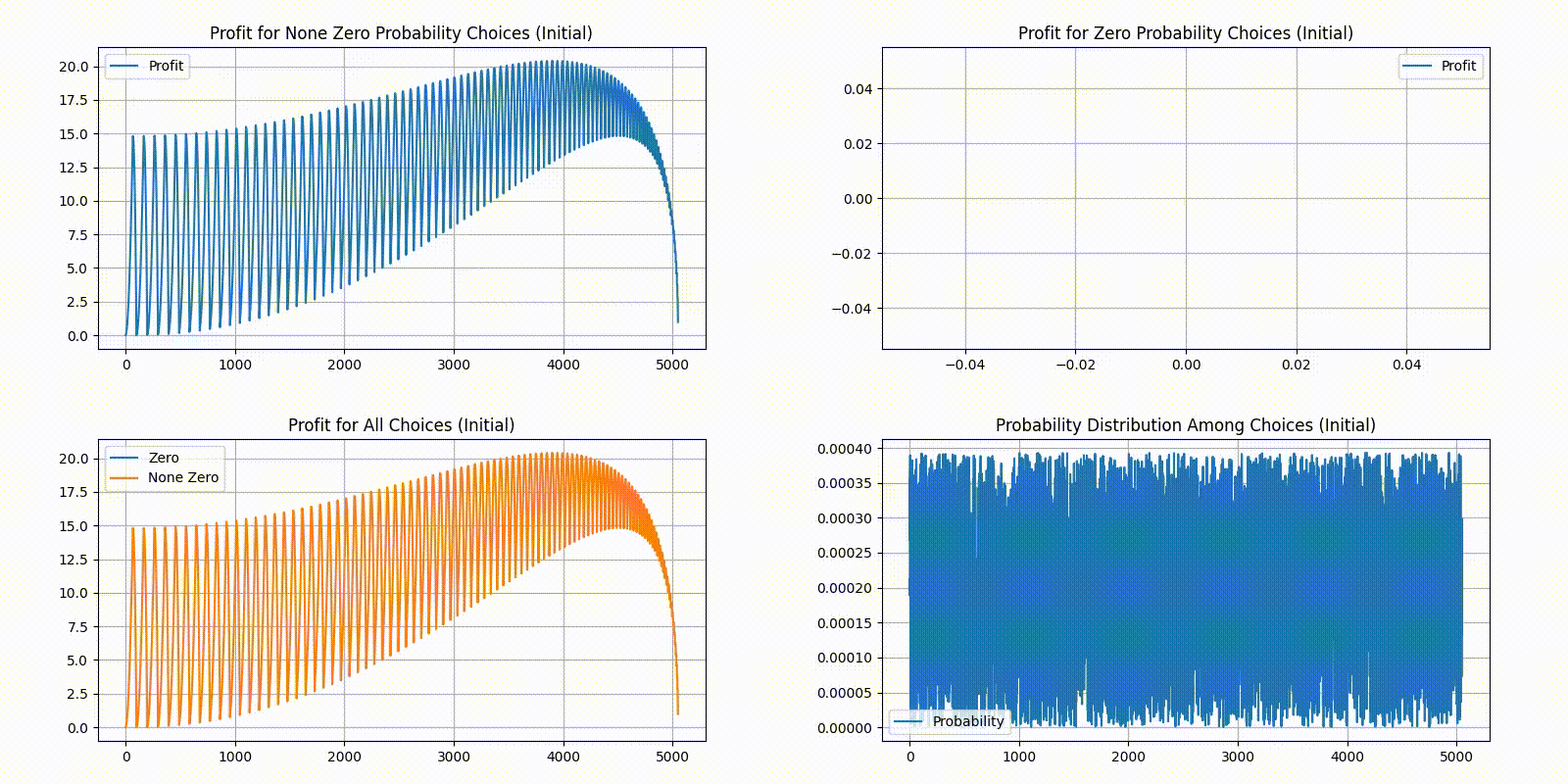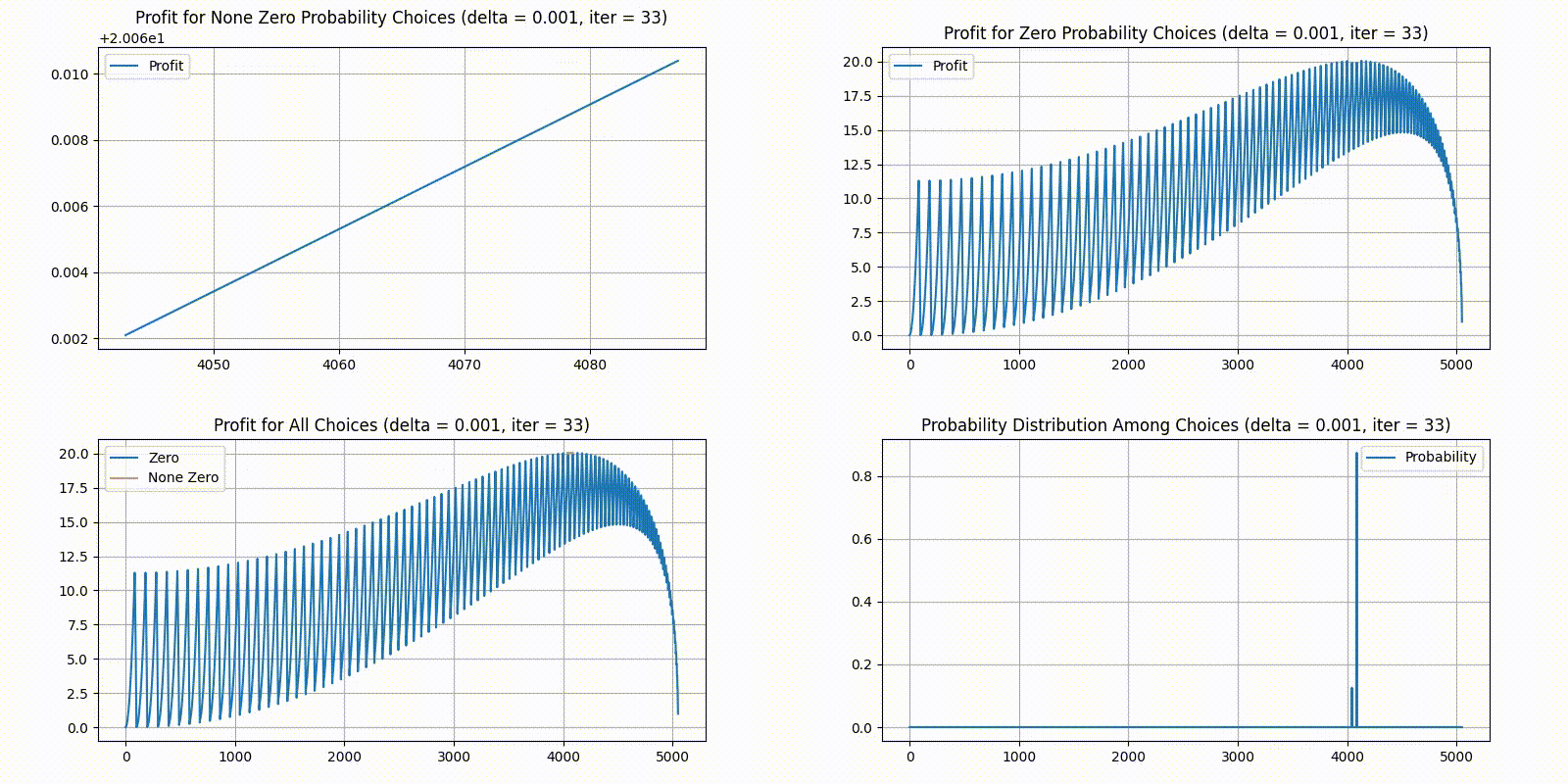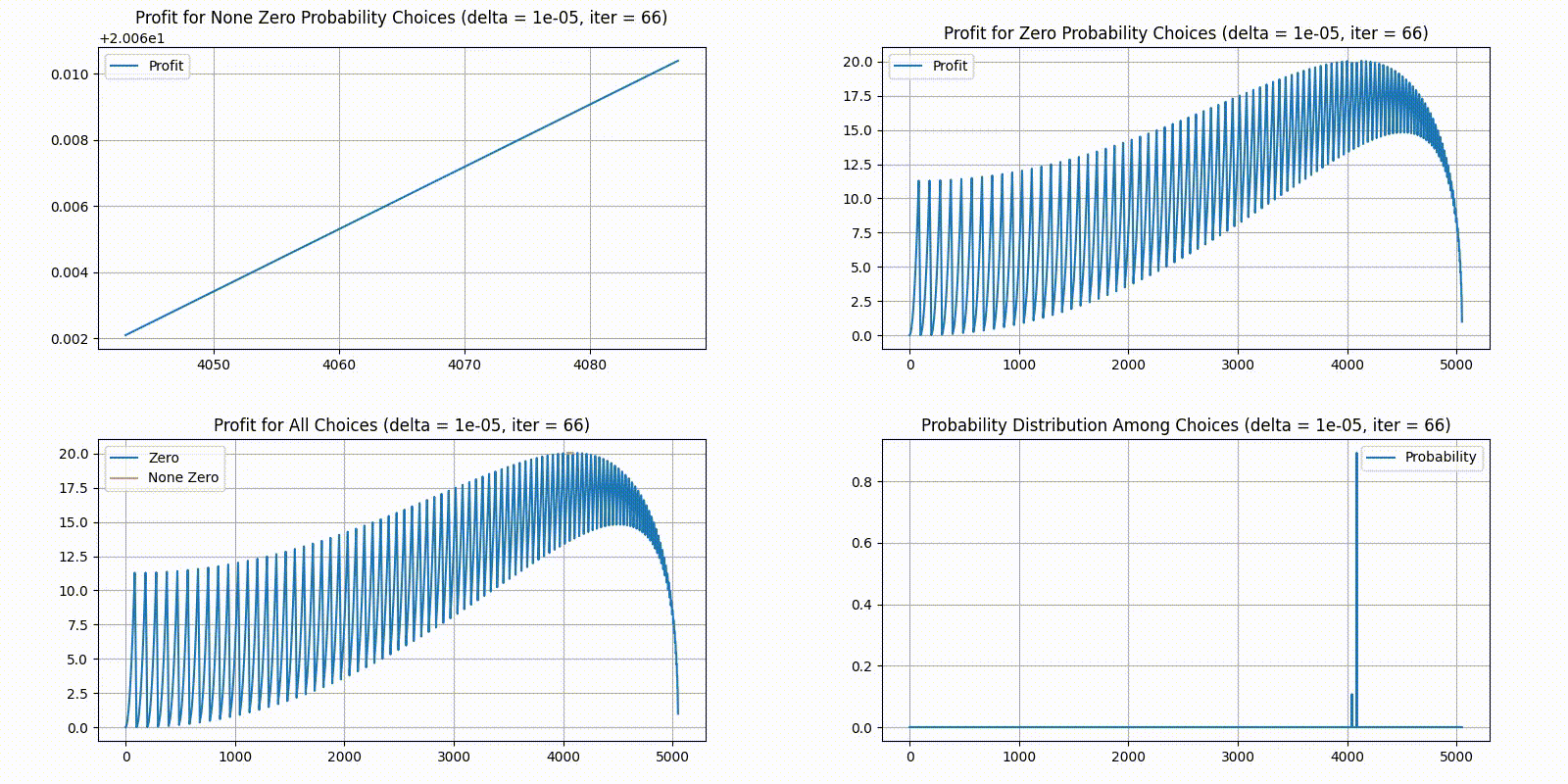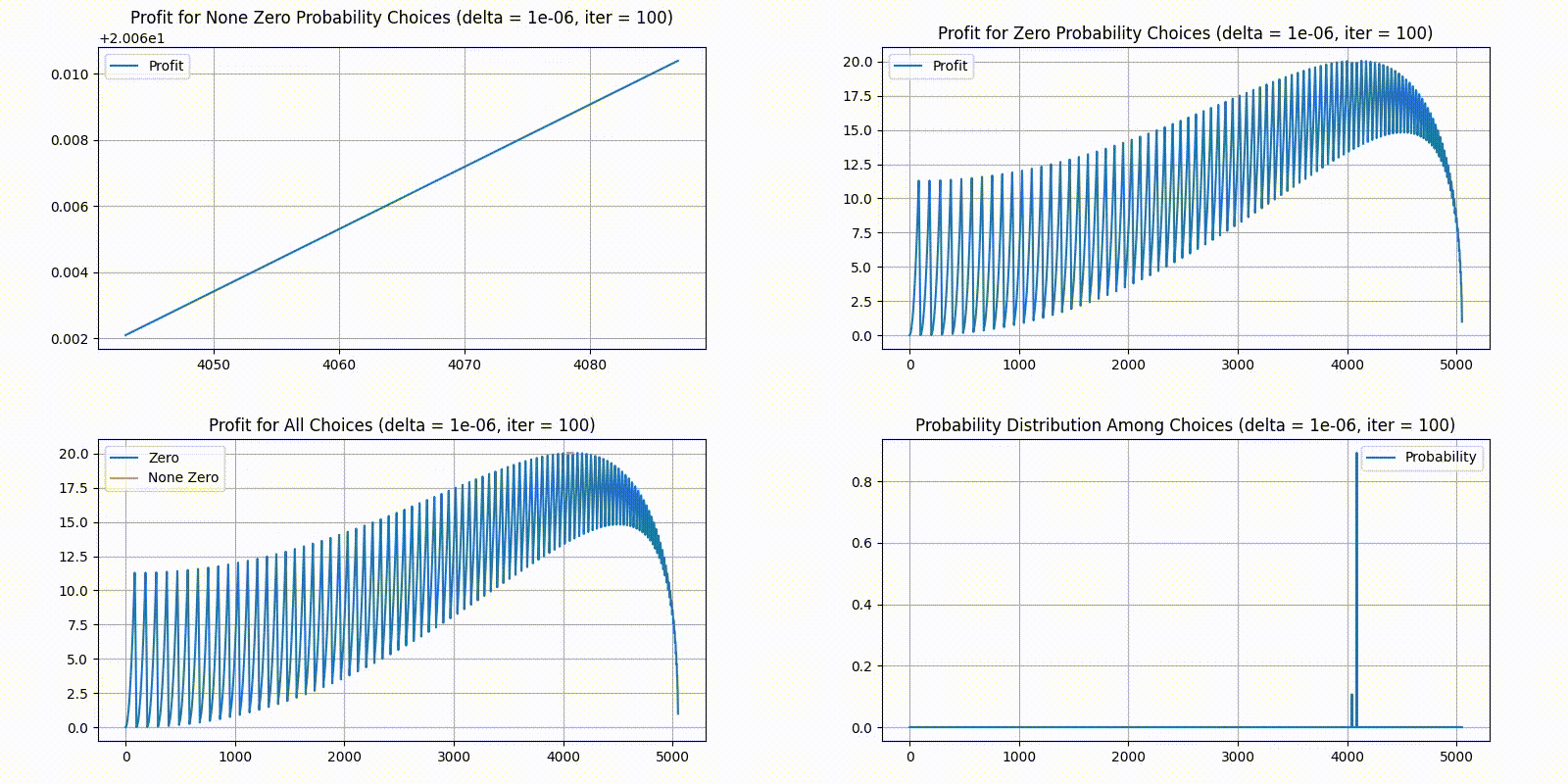
Unfortunately, the result is less interesting than we expected - there seems to be a clear optimal solution converging and not much back and forth. After 100 rounds, we were eventually left with just 2 choices with none zero probabilities. The distribution would probably converge to just one answer given more iterations or a higher step size $\delta$ . Here is our final statistics:

Top 10 none-zero choices:
[956, 984] 0.8930841506074441
[955, 984] 0.1069158493925551
----------------------------------------
Bottom 10 none-zero choices:
[955, 984] 0.1069158493925551
[956, 984] 0.8930841506074441

Additionally, there were people on discord claiming they will intentionally choose a low or high value in an attempt to artifitially influence the mean. As a result, we tested the most profitable solution given some people intentionally choosing the highest / lowest value / random value. It seems that the result is relatively stable, and small percentages of troll choices have minor influences that's generally not worth gambling for.

For 1.0% random choosers, with at least 0% choosing 900 and 0% choosing 1000, the best choice is:
Choice 4087 [956, 984] with probability 88% and profit 20.070400000000024
For 1.0% random choosers, with at least 5.0% choosing 900 and 0% choosing 1000, the best choice is:
Choice 4087 [956, 984] with probability 88% and profit 20.070400000000024
For 1.0% random choosers, with at least 0% choosing 900 and 5.0% choosing 1000, the best choice is:
Choice 4087 [956, 984] with probability 88% and profit 20.070400000000024
For 1.0% random choosers, with at least 10.0% choosing 900 and 0% choosing 1000, the best choice is:
Choice 4087 [956, 984] with probability 88% and profit 20.070400000000024
For 1.0% random choosers, with at least 0% choosing 900 and 10.0% choosing 1000, the best choice is:
Choice 4087 [956, 984] with probability 88% and profit 20.070400000000024
For 5.0% random choosers, with at least 0% choosing 900 and 0% choosing 1000, the best choice is:
Choice 4042 [955, 983] with probability 0% and profit 20.12500058734451
For 5.0% random choosers, with at least 5.0% choosing 900 and 0% choosing 1000, the best choice is:
Choice 4042 [955, 983] with probability 0% and profit 20.181300000000014
For 5.0% random choosers, with at least 0% choosing 900 and 5.0% choosing 1000, the best choice is:
Choice 4042 [955, 983] with probability 0% and profit 20.09472298578444
For 5.0% random choosers, with at least 10.0% choosing 900 and 0% choosing 1000, the best choice is:
Choice 4042 [955, 983] with probability 0% and profit 20.181300000000014
For 5.0% random choosers, with at least 0% choosing 900 and 10.0% choosing 1000, the best choice is:
Choice 4087 [956, 984] with probability 84% and profit 20.070400000000024
For 10.0% random choosers, with at least 0% choosing 900 and 0% choosing 1000, the best choice is:
Choice 4042 [955, 983] with probability 0% and profit 20.181300000000014
For 10.0% random choosers, with at least 5.0% choosing 900 and 0% choosing 1000, the best choice is:
Choice 4041 [955, 982] with probability 0% and profit 20.270700000000012
For 10.0% random choosers, with at least 0% choosing 900 and 5.0% choosing 1000, the best choice is:
Choice 4042 [955, 983] with probability 0% and profit 20.181300000000014
For 10.0% random choosers, with at least 10.0% choosing 900 and 0% choosing 1000, the best choice is:
Choice 4041 [955, 982] with probability 0% and profit 20.270700000000012
For 10.0% random choosers, with at least 0% choosing 900 and 10.0% choosing 1000, the best choice is:
Choice 4042 [955, 983] with probability 0% and profit 20.181300000000014

Round 4 Code

The full expanded code takes up too much space, so I made each code cell expandable. If you don't want to copy-paste each cell, here is a ready-to-run Colab Notebook with everything in it.

Import Libraries & Set Up Output Folder

import os
import cv2
import time
import json
import random
import imageio
import itertools

import numpy as np
import matplotlib.pyplot as plt

OUTPUT_NAME = "prosperity_240419_round4_manual_optimal_distribution_output"

try:
os.makedirs(OUTPUT_NAME)
except OSError:
if not os.path.isdir(OUTPUT_NAME):
raise

Define Constants

BETS = [i for i in range(900,1001)]
CHOICES = []
WEIGHTS = []

# Weights are the second choices. We use it to calculate the average
for c in itertools.combinations(BETS, 2):
    CHOICES.append(list(c))
    WEIGHTS.append(c[1])

WEIGHTS = np.array(WEIGHTS)

Helper Functions

# PDF for gold fish price
def f(x):
  return (x/5000) - (9/50)

# Integral of f, used to calculate G\_[a,b]

def int_f(a,b):
avg = (f(b)+f(a)) / 2
return (b-a) \* avg

# Function to simulate bids and calculate profits

def profit(v, i, mean):
a,b = CHOICES[i]
g1 = int_f(900, a)
g2 = int_f(a, b)

    if b == 1000:
      p = 1
    else:
      p = min(1, (1000-mean)/(1000-b))

    return ((1000-a) * g1) + ((1000-b) * g2 * p)

# Remaining are just plotting functions

def plot_none_zero_probability(v, name='Profit from choices with none zero probability'):
mean = np.dot(v, WEIGHTS)
x = [i for i in range(len(v)) if v[i]>0]
y = [profit(v, i, mean) for i in range(len(v)) if v[i]>0]

    plt.figure(figsize=(8, 4))
    plt.plot(x, y, label='Profit')
    plt.title(name)
    plt.grid(True)
    plt.legend()
    plt.savefig(f'{name}.png')

def plot_zero_probability(v, name='Profit from choices with zero probability'):
mean = np.dot(v, WEIGHTS)
x = [i for i in range(len(v)) if v[i]==0]
y = [profit(v, i, mean) for i in range(len(v)) if v[i]==0]

    plt.figure(figsize=(8, 4))
    plt.plot(x, y, label='Profit')
    plt.title(name)
    plt.grid(True)
    plt.legend()
    plt.savefig(f'{name}.png')

def plot_both_profit(v, name='Profit from both, in the same chart'):
mean = np.dot(v, WEIGHTS)

    x1 = [i for i in range(len(v)) if v[i]==0]
    y1 = [profit(v, i, mean) for i in range(len(v)) if v[i]==0]

    x2 = [i for i in range(len(v)) if v[i]>0]
    y2 = [profit(v, i, mean) for i in range(len(v)) if v[i]>0]

    plt.figure(figsize=(8, 4))
    plt.plot(x1, y1, label='Zero')
    plt.plot(x2, y2, label='None Zero')
    plt.title(name)
    plt.grid(True)
    plt.legend()
    plt.savefig(f'{name}.png')

def plot_probability(v, name='Probability Distribution among all possible choices'):
x = [i for i in range(len(v))]
y = [i for i in v]

    plt.figure(figsize=(8, 4))
    plt.plot(x, y, label='Probability')
    plt.title(name)
    plt.grid(True)
    plt.legend()
    plt.savefig(f'{name}.png')

def plot(v, n1, n2, n3, n4):
plot_none_zero_probability(v, n1)
plot_zero_probability(v, n2)
plot_both_profit(v, n3)
plot_probability(v, n4)

    image = cv2.vconcat([
        cv2.hconcat([cv2.imread(f'{n1}.png'), cv2.imread(f'{n2}.png')]),
        cv2.hconcat([cv2.imread(f'{n3}.png'), cv2.imread(f'{n4}.png')]),
    ])

    cv2.imwrite("result.png", image)
    plt.close("all")
    return imageio.v2.imread("result.png")

Run Simulation

# Initialize distribution vector with small random values summing to 1
random_values = np.random.rand(len(CHOICES))
v = random_values / np.sum(random_values)

mean = np.dot(v, WEIGHTS)

# The settings describe the delta iteration pairs
# (0.1, 20) means perform 20 iterations with delta=0.1
# After each delta iteration pair a checkpoint is saved
# Note that a iteration is described as iterating through all the pairs once
settings = np.array([
    (0.01, 20),
    (0.001, 20),
    (0.0001, 20),
    (0.00001, 20),
    (0.000001, 20),
])

# Time for logging and frames for plotting
init_time = time.time()
frame_lst = []

# Plotting
frame_lst.append(
    plot(
        v,
        "Profit for None Zero Probability Choices (Initial)",
        "Profit for Zero Probability Choices (Initial)",
        "Profit for All Choices (Initial)",
        "Probability Distribution Among Choices (Initial)"
    )
)

# Iterate through settings
counter = 0
checkpoint_counter = 0
for delta_value, num_iterations in settings:
    num_iterations = int(num_iterations)
    checkpoint_counter += num_iterations
    for iter in range(num_iterations):

        counter += 1

        # Time for logging
        round_time = time.time()

        # Iterate through pairs
        for i in range(len(v)):
            for j in range(len(v)):

                # Choose two different indices
                if i == j:
                    continue

                # Matrices soon become sparse, utilize it for speed boost
                if v[i]==0 and v[j]==0:
                    continue

                # Find profit, update probability accordingly
                profit_i = profit(v, i, mean)
                profit_j = profit(v, j, mean)

                # print(profit_i, profit_j)
                # print(CHOICES[i], CHOICES[j])
                # print(v[i], v[j])
                # print(mean)

                if profit_i < profit_j and v[i] > 0:
                    delta = min(v[i], delta_value)
                    v[i] -= delta
                    v[j] += delta
                    mean -= delta * WEIGHTS[i]
                    mean += delta * WEIGHTS[j]
                elif profit_i > profit_j and v[j] > 0:
                    delta = min(v[j], delta_value)
                    v[j] -= delta
                    v[i] += delta
                    mean -= delta * WEIGHTS[j]
                    mean += delta * WEIGHTS[i]

                # print(mean)

        # Logging
        mean = np.dot(v, WEIGHTS)
        max_index = np.argmax([profit(v, index, mean) for index, value in enumerate(v)])
        print(f"-"*40)
        print(f"Step Size = {delta_value} | Iteration {counter}/{checkpoint_counter}")
        print(f"Iteration Time:", time.strftime('%H hr %M min %S s', time.gmtime(time.time() - round_time)))
        print(f"Total Time:", time.strftime('%H hr %M min %S s', time.gmtime(time.time() - init_time)))
        print(f"Current mean is {np.dot(v, WEIGHTS)}, best choice is {CHOICES[max_index]} ({max_index}) with profit {profit(v, max_index, mean)}")

        # Plotting
        frame_lst.append(
            plot(
                v,
                f"Profit for None Zero Probability Choices (delta = {delta_value}, iter = {counter})",
                f"Profit for Zero Probability Choices (delta = {delta_value}, iter = {counter})",
                f"Profit for All Choices (delta = {delta_value}, iter = {counter})",
                f"Probability Distribution Among Choices (delta = {delta_value}, iter = {counter})"
            )
        )

    # Save Checkpoint
    with open(f'{OUTPUT_NAME}/checkpoint_{counter}.txt', 'w') as filehandle:
        json.dump(list(v), filehandle)

        imageio.mimsave(f'{OUTPUT_NAME}/checkpoint_{counter}.gif', frame_lst, fps=4, loop=2)

    print(f"-"*40)
    print(f"Updated checkpoint at iteration {counter}, saved to folder {OUTPUT_NAME}")

Get Statistics and Sample for Answer

def find_indices_by_count(weights, top_k, bottom_k):
    # Normalize the weights to sum to 1
    probabilities = weights / np.sum(weights)

    # Get indices sorted by probability
    sorted_indices = np.argsort(probabilities)[::-1]  # Descending order
    top_indices = sorted_indices[:top_k]

    # Filter out zero probabilities and get their indices
    non_zero_probabilities = probabilities[probabilities > 0]
    non_zero_sorted_indices = np.argsort(non_zero_probabilities)

    # Select the bottom k indices of non-zero probabilities
    if bottom_k > len(non_zero_sorted_indices):
        bottom_k = len(non_zero_sorted_indices)  # Adjust bottom_k if it's larger than available non-zero indices
    bottom_indices = non_zero_sorted_indices[:bottom_k]

    # Adjust the non-zero indices to match original array indices
    actual_bottom_indices = np.nonzero(probabilities > 0)[0][bottom_indices]

    return top_indices, actual_bottom_indices

def find_percentiles(v, i): # Ensure i is within the valid range
if i >= len(v) or i < 0:
return None # or raise an exception

    # Sort the entire array and find the position of v[i]
    sorted_v = np.sort(v)
    position_all = np.argwhere(sorted_v == v[i])[0][0]  # Using argwhere to find the first occurrence
    percentile_all = ((position_all + 0.5) / len(v)) * 100

    # Filter out zero entries and repeat the process
    non_zero_v = v[v != 0]
    sorted_non_zero_v = np.sort(non_zero_v)
    position_non_zero = np.argwhere(sorted_non_zero_v == v[i])[0][0]
    percentile_non_zero = ((position_non_zero + 0.5) / len(non_zero_v)) * 100

    return percentile_all, percentile_non_zero

top_indices, bottom_indices = find_indices_by_count(v, 10, 10)

print(f"-"\*40)
print("Top 10 choices:")
for i in top_indices:
print(CHOICES[i], v[i])

print(f"-"\*40)
print("Bottom 10 choices:")
for i in bottom_indices:
print(CHOICES[i], v[i])

print(f"-"\*40)
probabilities = v / np.sum(v)
answer = np.random.choice(len(v), p=probabilities)
print("Sampled Answer:", CHOICES[answer])
percentile_all, percentile_non_zero = find_percentiles(v, answer)
print(f"The answer is in the {percentile_all:.2f}th percentile among all entries.")
print(f"The answer is in the {percentile_non_zero:.2f}th percentile among non-zero entries.")

Simulate Troll Choices (Optional)

def check_random(v, weight=0.1, left=0., right=0.):

    if left<0 or right<0 or weight<0:
        raise Exception("weight, left, right must be non-negative values")
    if left+right>1 or weight>1:
        raise Exception("weight, left + right must be bounded by one")

    length = len(CHOICES)
    random_values = np.random.rand(length)

    random_values = (1-left-right) * random_values / np.sum(random_values)

    random_values[0] += left
    random_values[length-1] += right

    v_new = weight * random_values + (1-weight) * v
    mean_new = np.dot(v_new, WEIGHTS)

    # Initialize variables to track the maximum profit and the corresponding number
    max_profit = float('-inf')
    max_index = None

    # Iterate over each number in the array to calculate profit and find the maximum
    for i in range(length):
        current_profit = profit(v, i, mean_new)
        if current_profit > max_profit:
            max_profit = current_profit
            max_index = i


    print(f"For {weight * 100}% random choosers, with at least {left * 100}% choosing 900 and {right * 100}% choosing 1000, the best choice is:")
    print("Choice", max_index, CHOICES[max_index], f"with probability {int(v_new[max_index]*100)}% and profit {max_profit}")

    plot(
        v_new,
        f"None Zero Probability (random = {weight * 100}%, left={left * 100}%, right={right * 100}%)",
        f"Zero Probability (random = {weight * 100}%, left={left * 100}%, right={right * 100}%)",
        f"Best Choice is Choice {max_index} {CHOICES[max_index]} with profit {round(max_profit, 2)}",
        f"Probability Distribution Among Choices"
    )

    os.rename("result.png", os.path.join(OUTPUT_NAME, f"Random Test (random = {weight * 100}%, left={left * 100}%, right={right * 100}%).png"))

weight_lst = [0.01, 0.05, 0.1]
left_right_lst = [(0,0), (0.05,0), (0,0.05), (0.1,0), (0,0.1)]
num_tests = 3

for weight in weight_lst:
    for left, right in left_right_lst:
        check_random(v, weight, left, right)

Convert GIF to MP4 and Save Output (Optional, Colab Only)

!for f in prosperity_240419_round4_manual_optimal_distribution_output/*.gif; do ffmpeg -i "$f" -movflags faststart -pix_fmt yuv420p -vf "scale=trunc(iw/2)*2:trunc(ih/2)*2" -c:v libx264 -preset fast -crf 23 "${f%.*}.mp4"; done

import shutil
shutil.make_archive(OUTPUT_NAME, "zip", OUTPUT_NAME)

from google.colab import files
files.download(f'{OUTPUT_NAME}.zip')